В геометрии понятие перпендикулярных углов имеет особое значение. Рассмотрим основные свойства и суммы, связанные с перпендикулярными углами.
Содержание
Определение перпендикулярных углов
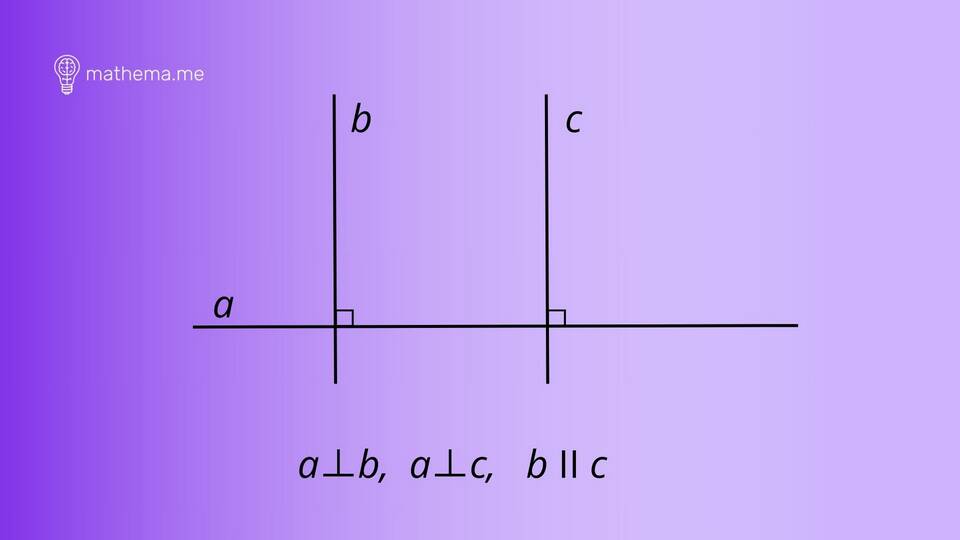
Перпендикулярные углы - это углы, образованные пересечением двух прямых линий под углом 90 градусов. Основные характеристики:
- Каждый из четырех углов при пересечении перпендикулярных прямых равен 90°
- Перпендикулярные прямые образуют прямой угол
- Такие углы называются конгруэнтными
Сумма перпендикулярных углов
| Тип углов | Сумма |
| Два смежных перпендикулярных угла | 180° (образуют развернутый угол) |
| Четыре угла при пересечении перпендикулярных прямых | 360° |
| Один перпендикулярный угол | 90° |
Свойства перпендикулярных углов
- Все четыре угла при пересечении перпендикулярных прямых равны между собой
- Биссектриса перпендикулярного угла делит его на два угла по 45°
- Перпендикулярные углы сохраняют свою величину при параллельном переносе
Практическое применение
Знание суммы перпендикулярных углов важно для:
- Построения геометрических фигур
- Расчета параметров в архитектуре
- Проектирования технических конструкций
- Решение задач по геометрии
Дополнительные сведения
В трехмерном пространстве понятие перпендикулярности распространяется на плоскости и прямые. Сумма углов между тремя взаимно перпендикулярными плоскостями составляет 270° (по 90° между каждой парой).
Таким образом, сумма перпендикулярных углов зависит от их количества и взаимного расположения, но всегда основывается на фундаментальном свойстве перпендикулярности - угле в 90 градусов.